Programozó versenyekMagas szintű programozási nyelvek 1, egyéni verseny, 2012. április 22.
2012. április 22. 10:15 –
2012. április 22. 15:15
|
Riemann-összegek
Az integrálszámítás olyan problémákkal foglalkozik, amelyek „egy görbe alatti terület meghatározásával” oldhatók meg. Ez azt jelenti, hogy van egy valós számokat valós számokra képező f függvényünk, egy a alsó korlátunk, egy b felső korlátunk, és szeretnénk meghatározni annak az alakzatnak a területét, amelyet balról az x = a egyenlettel leírt egyenes, jobbról az x = b egyenlettel leírt egyenes, alulról az x tengely (azaz az y = 0 egyenlettel leírt egyenes), felülről pedig az f függvény által meghatározott görbe határol.
A kalkulus módszereinek felhasználásával gyakran pontosan megadható ez a terület. Azokban az esetekben, amikor mégsem, a terület Riemann-összegnek nevezett közelítésének a kiszámítására hagyatkozunk.
A számítást úgy hajtjuk végre, hogy választunk egy m pozitív egész számot, majd egymás mellé helyezünk ∆x = (b − a) / m szélességű téglalapokat az x = a és az x = b egyenesek között. (A téglalapok bal oldali élei tehát az x = a, x = a + ∆x, x = a + 2∆x, x = a + 3∆x stb. egyenesekre esnek.) Az egyes téglalapok magasságát úgy választjuk meg, hogy a bal felső csúcsuk a görbére essen. Ezután kiszámítjuk a téglalapok területeinek az összegét, amely megadja a kérdéses alakzat területének egy becslését. (Általában igaz, hogy minél nagyobbra választjuk m értékét, annál pontosabb becslésre számíthatunk.)
Példaként tekintsük a következő ábrát, amelyen a = 0, b = 16, m = 8, f-et pedig a görbe szemlélteti.
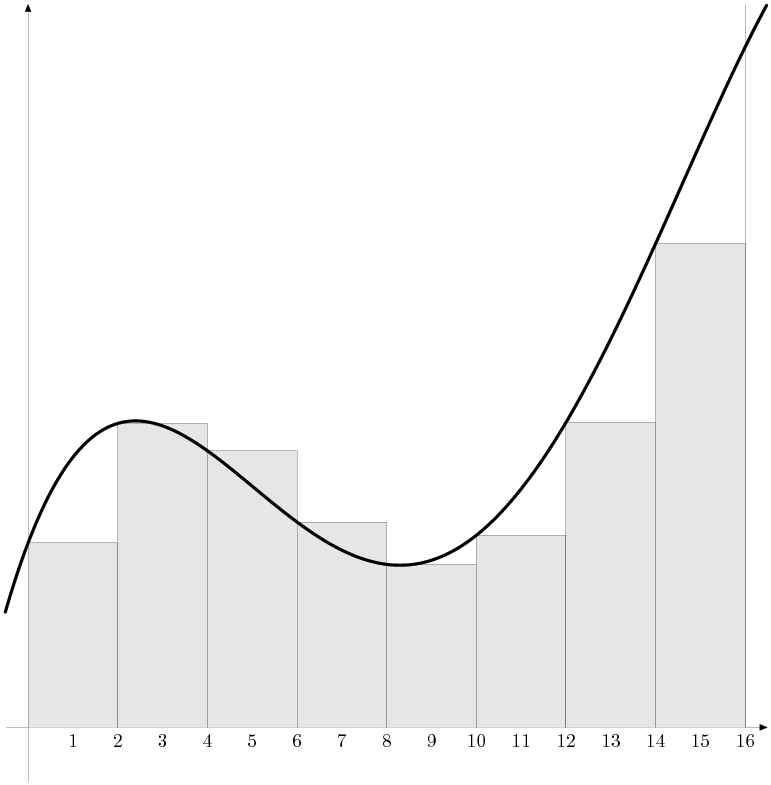
1. ábra: Görbe alatti terület becslése Riemann-összeggel
Írj programot, amely bemenetként megkap egy a és egy b valós számot (ahol a < b), egy m pozitív egész számot, valamint egy p polinom leírását (amelyre p(x) ≥ 0 teljesül minden x ∊ [a, b] esetén), és a fent leírt módszerrel megbecsli annak az alakzatnak a területét, amelyet balról az x = a egyenes, jobbról az x = b egyenes, alulról az y = 0 egyenes, felülről pedig p határol.
Vedd figyelembe, hogy egy p(x) polinom valójában egy olyan függvény, amely kifejezhető
formában, valamely k ≥ 0 egész érték és c0, c1, …, ck valós számok (együtthatók) esetén, ahol k-t p fokának nevezzük.
A bemenet specifikációja
Az első sor egy n pozitív egész számot tartalmaz, és azoknak az alakzatoknak a számát adja meg, amelyeknek meg kell becsülni a területét. A következő n sor mindegyikében egy-egy alakzat leírása található. Egy alakzat az a és b valós számokkal (az alsó és felső határokkal), egy m pozitív egész számmal (a területbecslés kiszámításához használt téglalapok számával), egy k nemnegatív egész számmal (a polinom fokszámával), valamint a polinom k + 1 együtthatójával (c0-tól ck-ig) van megadva.
A kimenet specifikációja
A bemeneten megadott minden alakzatra egy-egy kétsoros üzenetet kell a kimenetre írni, amely megadja a polinomot, a határokat, a területbecslés kiszámításához használt téglalapok számát és magát a becslést. Minden valós értéket pontosan egy tizedesjegy pontossággal kell kiírni. Lásd alább a példa kimenetet a pontos formátumért. Minden üzenet után írj ki egy üres sort!
Példa bemenet
30.0 4.0 4 1 0.0 2.00.0 4.0 8 1 0.0 2.0-3.0 1.0 4 2 2.0 0.0 1.0
A példa bemenethez tartozó kimenet
Estimated area under y = 0.0x^0 + 2.0x^1between x = 0.0 and x = 4.0 using 4 rectangles is 12.0Estimated area under y = 0.0x^0 + 2.0x^1between x = 0.0 and x = 4.0 using 8 rectangles is 14.0Estimated area under y = 2.0x^0 + 0.0x^1 + 1.0x^2between x = -3.0 and x = 1.0 using 4 rectangles is 22.0