Incircles Again

In the figure below, you can see a triangle ABC and its incircle (circle that touches all the sides of a triangle internally). The radius of this incircle is r. Three other circles are drawn. Each of them touches two sides of this triangle and the incircle of ABC. The radiuses of these circles are r₁, r₂, and r₃.

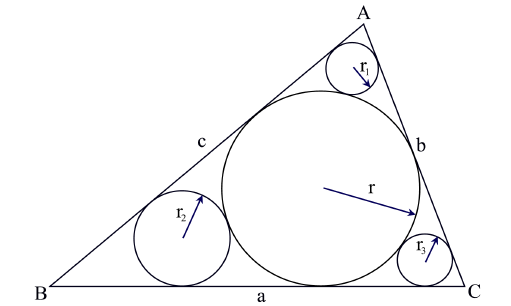
Given the values of r, r₁, r₂, and r₃, you will have to find the area of triangle ABC.

Input Specification

The input can contain up to 1000 lines of data. Each line contains four positive floating-point numbers which denote the values of r, r₁, r₂, and r₃, respectively.

The input is terminated by a line containing four negative integers.

Output Specification

For each line of input, produce one line of output. This line contains the sequence number of the test case followed by a floating-point number which denotes the area of triangle ABC. This floating-point number must have two digits after the decimal point. You can assume that for the given values of r, r₁, r₂, and r₃, it will always be possible to construct a triangle ABC. If required, you can assume that π = 3.141592653589793, and also use double precision floating-point numbers for floating-point calculations. You can assume that there will be no such input for which small precision errors would cause difference in the printed output. Look at the output for sample input for details.

Sample Input

1. 49.1958415692 5.3025839959 20.7869367050 31.8019699761
2. 186.6830516757 71.9474500429 84.8796672233 37.6219288070
3. -1 -1 -1 -1

download as text file

Output for Sample Input

1. Case 1: 18237.14
2. Case 2: 195777.32

download as text file