As Long as I Learn, I Live

What makes problem solving so interesting? What makes it challenging? Why do we put so much effort in it but never get bored? For us (problem-setters), it's like “As long as I learn, I live!” We learn so many beautiful things, we find great ideas and techniques, and there is no end to it.

In this problem, you are given a person's life stages in graph form. There are n nodes in the graph. Nodes represent stages, numbered from 0 to n – 1, and edges represent that he can move from one stage to another. 0th node is the node where he starts his journey. You may have guessed: there will be no cycles in the graph (no one can go back to past!).

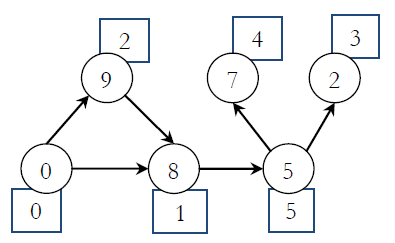
A value x is attached to each node; it means he will learn x units if he comes into this node. For example, the graph in the picture represents a person's life stages. The circles represent the nodes, the value in a circle represents the value that will be gained if the person comes into this node. The numbers in rectangular boxes represent the node ids. If the person reaches the 1st node, he will learn 8 added units, if he reaches the 4th node, he will learn 7 added units.

As in real life, no one knows the future, but can predict some common things in near future. If the person is in node u, he only knows the nodes that have an edge from u. The person wants to learn more, that's why he always takes the stage that looks better, i.e., has a maximum value. So, if he is in node 0, he only knows the learning units in node 1 and 2, but doesn't know about nodes 3, 4, or 5. He will prefer node 2 over node 1 (because node 2 will give him 9 learning units). He continues the journey with this method. He can finish at any stage, but will try to learn more. You can assume that the graph is given such that from any node, the next node can be picked deterministically, i.e., for any node u, there will be exactly one node v which has the maximum value, and there is an edge from u to v.

Input Specification

The input starts with an integer T (T ≤ 100), denoting the number of test cases.

Each test case starts with a blank line. The next line contains two integers n (2 ≤ n ≤ 100) and m (n – 1 ≤ m ≤ n * (n – 1) / 2). n denotes the number of nodes in the graph, and m denotes the number of edges in the graph. The next line contains n space-separated integers denoting the learning units in the respective nodes. The values will be between 1 and 1000 (inclusive) except the 0th node, which will have a value of 0. Each of the next m lines contains two integers u and v (0 ≤ u, v < n, u ≠ v) meaning that there is a directed edge from u to v. You can safely assume that the given graph will follow the restrictions described above. From the 0th node, it will be possible to reach any node. There will be at most one edge between any pair of nodes.

Output Specification

For each test case, print the case number, the maximum total learning units the person can gain (following the strategy mentioned above), and the node id where the person ends the journey.

Sample Input

1. 1
2.  
3. 6 6
4. 0 8 9 2 7 5
5. 5 4
6. 5 3
7. 1 5
8. 0 1
9. 0 2
10. 2 1

download as text file

Output for Sample Input

1. Case 1: 29 4

download as text file