Amíg tanulok, életben vagyok

Mitől olyan érdekes a feladatmegoldás? Miért kihívás? Miért fordítunk rá annyi energiát, és mégsem unjuk meg? Mi (a feladatsor összeállítói) ezt úgy tudnánk kifejezni, hogy „amíg tanulunk, életben vagyunk”. Annyi csodálatos dolgot tanulunk, annyi nagyszerű ötlettel és technikával találkozunk, és sosem érnek véget!

Ebben a feladatban egy személy életszakaszai lesznek megadva egy gráf formájában. A gráfnak n csomópontja van. A csomópontok az életszakaszokat reprezentálják, amelyeket 0-tól n – 1-ig sorszámozunk, az élek pedig azt jelölik, hogy a személy átléphet az egyik életszakaszából egy másikba. A 0. csomópont az a csomópont, ahol megkezdi az utazását. Kitalálhattad: a gráfban nem lesznek körök (senki sem mehet vissza a múltba!).

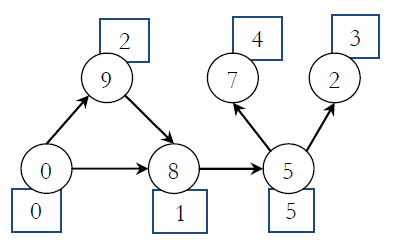
Minden csomóponthoz egy x érték van hozzárendelve; ez azt jelenti, hogy x egységnyit tanul, ha ebbe a csomópontba lép. Az ábrán látható gráf például egy személy életszakaszait illusztrálja. A körök a csomópontokat jelölik, egy körbe írt szám pedig azt az értéket adja meg, amennyit a személy szerez, ha az adott csomópontba lép. A négyzetekbe írt számok a csomópont-azonosítók. Ha például a személy az 1-es csomópontba lép, 8 további egységet tanul, ha a 4-es csomópontba, akkor pedig 7-et.

Ahogy a valós életben, senki sem ismeri a jövőt, de megjósolhatunk bizonyos dolgokat a közeljövőre vonatkozóan. Ha a személy az u csomópontban van, akkor csak azokat a csomópontokat ismeri, amelyekbe vezet él u-ból. Mivel a lehető legtöbbet szeretne tanulni, ezért mindig a legkecsegtetőbb életszakaszt választja, azaz azt, amelyik a legnagyobb értékkel rendelkezik. Ha tehát a 0. csomópontban van, akkor csak az 1-es és 2-es csomópontokhoz tartozó értékeket ismeri, és semmit sem tud a 3-as, a 4-es és az 5-ös csomópontokról. A 2-es csomópontot választja az 1-es helyett (mert a 2-es csomópont 9 tanulási egységet biztosít a számára). Ezután folytatja az útját ugyanezzel a módszerrel. Bármelyik szakaszban megállhat, de mindig megpróbál tovább tanulni. Feltételezheted, hogy a gráf bármelyik csomópontjából a következőt determinisztikusan lehet kiválasztani, azaz bármelyik u csomóponthoz pontosan egy olyan v csomópont létezik, amelynek az értéke maximális, és létezik él u-ból v-be.

A bemenet specifikációja

A bemenet egy T egész számmal kezdődik, amely a tesztesetek számát adja meg (T ≤ 100).

Minden teszteset egy üres sorral kezdődik. A következő sor két egész számot tartalmaz: n-et (2 ≤ n ≤ 100) és m-et (n – 1 ≤ m ≤ n * (n – 1) / 2). n jelöli a gráf csomópontjainak, m pedig az éleinek a számát. A következő sor n egész számból áll egy-egy szóközzel elválasztva, amelyek a megfelelő csomóponthoz rendelt tanulási egységeket adják meg. Az értékek 1 és 1000 közé esnek, kivéve a 0. csomópontot, amelyhez mindig a 0 érték lesz hozzárendelve. A következő m sor mindegyike két egész számot tartalmaz: u-t és v-t (0 ≤ u, v < n, u ≠ v), amelyek azt jelölik, hogy létezik irányított él u-ból v-be. Feltételezheted, hogy a gráf eleget tesz a fent leírt megszorításoknak. A 0. csomópontból bármelyik csomópontba el lehet jutni, és legfeljebb egy él lesz bármely két csomópont között.

A kimenet specifikációja

Minden tesztesetre a kimenetre kell írni a teszteset sorszámát, a személy által szerezhető tanulási egységek összegének a maximumát (a fent leírt stratégiát követve), valamint annak a csomópontnak az azonosítóját, amelyikben befejezte az utazását.

Példa bemenet

1. 1
2.  
3. 6 6
4. 0 8 9 2 7 5
5. 5 4
6. 5 3
7. 1 5
8. 0 1
9. 0 2
10. 2 1

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. Case 1: 29 4

letöltés szöveges állományként