Stern–Brocot-fa

A számelméletben a Stern–Brocot-fa egy módszer az összes nemnegatív racionális szám és egy, a végtelent reprezentáló (itt formálisan 1/0-val jelölt) pont felsorolására.

A fát egy iteratív eljárással állíthatjuk elő. A legegyszerűbben egy listaként írható le. Kiindulunk a {0/1, 1/0} listából, ahol 0/1 a 0-t, 1/0 pedig a végtelent reprezentálja, majd bármely két tört közé beírjuk a két tört mediánsát (az a/c és a b/d törtek mediánsa az (a + b)/(c + d) tört). Az eljárás első néhány lépése a következő listákat eredményezi:

{0/1, 1/0}
{0/1, 1/1, 1/0}
{0/1, 1/2, 1/1, 2/1, 1/0}
{0/1, 1/3, 1/2, 2/3, 1/1, 3/2, 2/1, 3/1, 1/0}

Ezt az eljárást egy olyan fával ábrázolhatjuk, amelyben a sorok az egyes lépésekben hozzáadott új számoknak felenek meg.

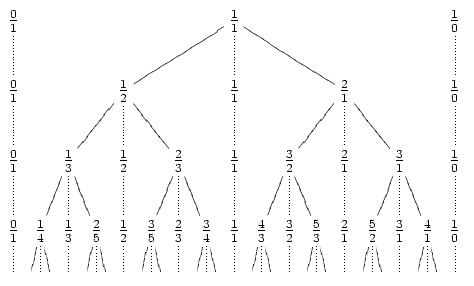
Forrás: Wikipedia

A fában egy tört pozícióját megadhatjuk egy, a fa gyökeréből (az 1/1 törtből) kiinduló, bal (L) és jobb (R) mozgásokból álló úttal. A feladatod, hogy meghatározd azt a törtet, amely egy adott úthoz tartozik.

A bemenet specifikációja

A bemenet első sora egy N egész számot, a tesztesetek számát tartalmazza (0 < N ≤ 10000). A következő N sor mindegyike egy utat ír le a fában. Az út egy legfeljebb 90 karakterből álló karaktersorozat, amely „L” vagy „R” karakterekből áll.

A kimenet specifikációja

Minden tesztesetre egy sort kell a kimenetre írni az alábbi formában: „a/b”, ahol a az út által meghatározott tört számlálója, b pedig a nevezője.

Példa bemenet

1. 3
2. RL
3. RLR
4. RRL

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. 3/2
2. 5/3
3. 5/2

letöltés szöveges állományként