Alternative Arborescence

Given a graph, we define “proper coloring” as coloring of the graph nodes in such a way that no two adjacent nodes have the same color. If we map each color to a positive integer, we can calculate the sum of all colors assigned to the graph.

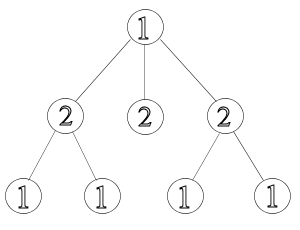
In this problem, you will be given a tree (connected graph with no simple loops). Can you determine the minimum color sum that can be achieved when the tree is properly colored? The image below shows a proper coloring of the second example tree with a sum of 11:

Input Specification

The input consists of several test cases. Each test case starts with n (1 ≤ n ≤ 10000), the number of nodes in the tree. The next n lines will be of the form “u: v₁ v₂ … v_k”, where u is the root of a subtree, and v_i's are its children (0 ≤ u, v_i ≤ n – 1).

Every test case will be followed by a blank line. The input ends with a case where n = 0, which should not be processed.

Output Specification

For each test case, print the minimum sum of colors that can be achieved by some proper coloring of the tree.

Sample Input

1. 2
2. 0:
3. 1: 0
5. 8
6. 0: 1 2 3
7. 1: 4 5
8. 2:
9. 3: 6 7
10. 4:
11. 5:
12. 6:
13. 7:
15. 0

download as text file

Output for Sample Input

1. 3
2. 11

download as text file