Színes fák

Egy gráf „jó színezése” alatt a gráf csúcsainak egy olyan színezését értjük, amelyben az összekötött csúcsok különböző színeket kapnak. Ha minden egyes színhez hozzárendelünk egy pozitív egész számot, kiszámíthatjuk a gráf csúcsaihoz rendelt színek összegét.

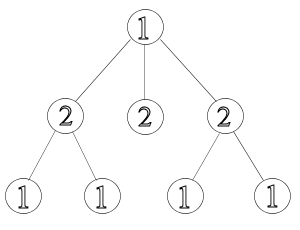
Ebben a feladatban egy fa (hurokmentes összefüggő gráf) lesz megadva. Meg tudnád határozni azt a legkisebb színösszeget, amelyet a fa jó színezéseivel megkaphatunk? Az alábbi ábra a második példában leírt fa egy jó színezését mutatja, ahol az összeg 11:

A bemenet specifikációja

A bemenet számos tesztesetet tartalmaz. Minden teszteset n-nel, a fa csúcsainak a számával kezdődik (1 ≤ n ≤ 10000). A következő n sor „u: v₁ v₂ … v_k” alakú, ahol u egy részfa gyökere, a v_i-k pedig a gyermekei (0 ≤ u, v_i ≤ n – 1).

Minden tesztesetet egy üres sor követ. A bemenet egy olyan tesztesettel zárul, amelyben n = 0; ezt a tesztesetet nem kell feldolgozni.

A kimenet specifikációja

Minden tesztesetre a fa jó színezéseivel elérhető minimális színösszeget kell a kimenetre írni külön sorban.

Példa bemenet

1. 2
2. 0:
3. 1: 0
5. 8
6. 0: 1 2 3
7. 1: 4 5
8. 2:
9. 3: 6 7
10. 4:
11. 5:
12. 6:
13. 7:
15. 0

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. 3
2. 11

letöltés szöveges állományként