Programming contestsDEIK Regionális Programozó Csapatverseny, középiskolai kategória, 2013. december 1.
December 1, 2013, 10:30 AM –
December 1, 2013, 3:30 PM
|
Stern–Brocot Tree
In number theory, the Stern–Brocot tree is a method of listing all nonnegative rational numbers as well as a point representing infinity (here represented formally as 1/0).
The tree may be created by an iterative process. It is easiest to describe as a list. Beginning with the list {0/1, 1/0}, representing 0 and infinity respectively, one places between any two fractions the mediant of the fractions (the mediant of a/c and b/d is (a + b)/(c + d)). The first few steps of this process yield:
{0/1, 1/0}
{0/1, 1/1, 1/0}
{0/1, 1/2, 1/1, 2/1, 1/0}
{0/1, 1/3, 1/2, 2/3, 1/1, 3/2, 2/1, 3/1, 1/0}
This process can be represented as a tree where each row corresponds to the new numbers added at each step:
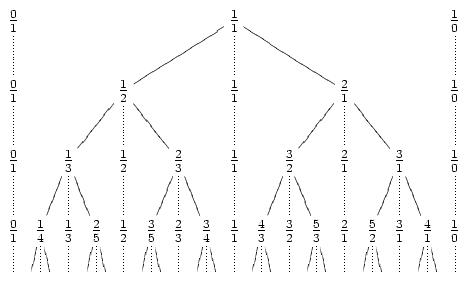
From Wikipedia
The position of a fraction in the tree can be specified as a path consisting of left
(L) and right (R) moves along the tree starting from the top
(fraction 1/1). You have to find a fraction based on a given path.
Input Specification
The first line of the input contains an integer N
(0 < N ≤ 10000), the number of test cases. Each of the
next N lines contains a path in the tree. A path is a string of at most 90 characters,
consisting of characters “L” or “R”.
Output Specification
For each test case, print one line formatted like this: “a/b”, where a is the numerator, and b is the denominator of the fraction represented by the path.
Sample Input
3RLRLRRRL
Output for Sample Input
3/25/35/2