Programming contestsDEIK Regionális Programozó Csapatverseny, egyetemi/főiskolai kategória, 2013. december 1.
December 1, 2013, 10:30 AM –
December 1, 2013, 3:30 PM
|
Hardly Hard
You have been given the task of cutting a quadrilateral slice of cake out of a larger, rectangular cake. You must find the slice with the smallest perimeter that satisfies the following constraints. If the cake is of size 10000-by-10000 units and is represented using the first quadrant of the Cartesian plane, then your slice is the quadrilateral ABCD (see figure).
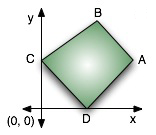
Points A and B are fixed and will be given to you. Also, A and B will lie on a negatively sloping line. Furthermore, points C and D must lie on the positive y-axis and positive x-axis, respectively, but it is up to you to determine where these two points should be. A, B, C, and D will be distinct points.
Output the minimum perimeter of your slice of cake.
Input Specification
On the first line, you will be given n (1 ≤ n ≤ 100), the number of test cases. The following n lines each contain ax ay bx by (0 < ax, ay, bx, by ≤ 10000.0), the coordinates of points A and B, respectively.
Output Specification
For each test case, output the perimeter accurate to 3 decimal places on its own line.
Sample Input
13.0 1.0 1.0 2.0
Output for Sample Input
7.236