Programming contestsDEIK Regionális Programozó Csapatverseny, egyetemi/főiskolai kategória, 2013. december 1.
December 1, 2013, 10:30 AM –
December 1, 2013, 3:30 PM
|
The Stern–Brocot Number System
The Stern–Brocot tree is a beautiful way for constructing the set of all nonnegative fractions m/n, where m and n are relatively prime. The idea is to start with two fractions (0/1, 1/0) and then repeat the following operation as many times as desired:
Insert (m + m')/(n + n') between two adjacent fractions m/n and m'/n'.
For example, the first step gives us one new entry between 0/1 and 1/0:
0/1, 1/1, 1/0
The next step gives two more:
0/1, 1/2, 1/1, 2/1, 1/0
The next gives four more:
0/1, 1/3, 1/2, 2/3, 1/1, 3/2, 2/1, 3/1, 1/0
Then we will get 8, 16, and so on. The entire array can be regarded as an infinite binary tree structure whose top levels look like this:
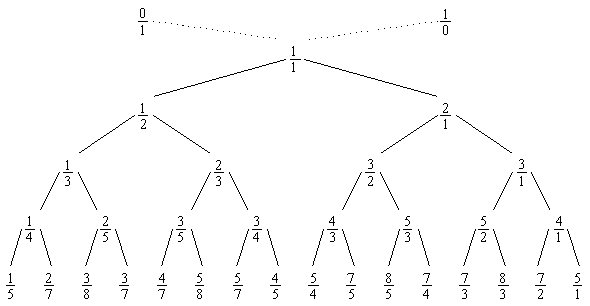
The construction preserves order, and we couldn't possibly get the same fraction in two different places.
We can, in fact, regard the Stern–Brocot tree as a number system for representing rational numbers because each positive, reduced fraction occurs exactly once. Let's use the letters L and R to stand for going down to the left or right branch as we proceed from the root of the tree to a particular fraction; then a string of Ls and Rs uniquely identifies a place in the tree. For example, LRRL means that we go left from 1/1 down to 1/2, then right to 2/3, then right to 3/4, then left to 5/7. We can consider LRRL to be a representation of 5/7. Every positive fraction gets represented in this way as a unique string of Ls and Rs.
Well, actually there's a slight problem: The fraction 1/1 corresponds to the empty string, and we need a notation for that. Let's agree to call it I, because that looks something like 1, and it stands for “identity”.
In this problem, given a positive rational fraction, you are expected to represent it in Stern–Brocot number system.
Input Specification
The input contains multiple test cases. Each test case consists of a line containing two 32-bit positive integers m and n, where m and n are relatively prime. The input terminates with a test case containing two 1s for m and n, and this case must not be processed.
Output Specification
For each test case in the input, output a line containing the representation of the given fraction in the Stern–Brocot number system.
Sample Input
5 7878 3231 1
Output for Sample Input
LRRLRRLRRLRLLLLRLRRR