Lee-távolság

Az információelméletben két azonos (n) hosszúságú kód (sztring) q elemű abécé (0,1,...,q-1) (ahol q>=2) feletti Lee-távolságán az alábbi összeget értjük:

Például egy hatelemű (0 és 5 közötti elemek feletti) ábécé esetén a 3140 és a 2543 közötti Lee-távolság 6, mivel min(|3-2|,6-|3-2|)=1, min(|1-5|,6-|1-5|)=2, min(|4-4|,6-|4-4|)=0, min(|0-3|,6-|0-3|)=3, és 1+2+0+3=6. Egy szótár (szavak halmaza) minimális Lee-távolságán a szótár bármely két szava közötti Lee-távolságok minimumát értjük. Készítsen programot, amely meghatározza egy szótár minimális Lee-távolságát!

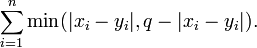
A bemenet specifikációja

A bemenet első sorában két egész helyezkedik el. Az első az abécé különböző betűinek száma (q), ahol 2 <= q <= 10, tőle pontosan egy szóközzel elválasztva pedig a szótár szavainak száma (egynél nagyobb pozitív egész). A bemenet további soraiban soronként egy szótári szó jelenik meg. Feltételezzük, hogy a szótár szavai azonos hosszúságúak, és csak számjegyeket tartalmaznak!

A kimenet specifikációja

A kimenet egyetlen sorból áll, amelyben egyetlen szám, a kiszámított minimális Lee-távolság jelenik meg.

Példa bemenet

1. 6 3
2. 3140
3. 2543
4. 1111

letöltés szöveges állományként

Példa kimenet

1. 6

letöltés szöveges állományként