Programming contestsDEIK Regionális Programozó Csapatverseny, középiskolai kategória, 2014. november 30.
November 30, 2014, 10:30 AM –
November 30, 2014, 3:30 PM
|
Track Smoothing
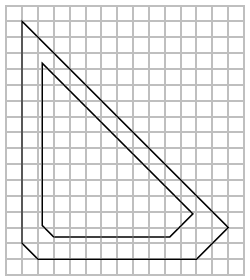
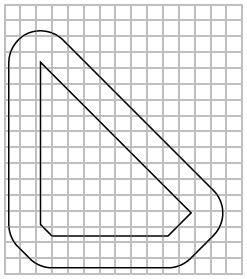
Bob has the task to plan a racing track of a specific length. He thought it was a great idea to just form a convex polygon that has exactly the required perimeter. However, he was told that racing cars cannot drive such sharp corners like in his plan.
He has to ensure some minimal radius for all curves in his track. Bob loves the shape of his track, so he doesn't want to change it too much. His plan is to scale the track down around the balance point of the polygon that specifies his track. Then, he wants to draw the new track with a line that has a constant distance to the scaled track. The chosen distance should be the minimum distance that fulfils the given minimum radius constraint. He asks you to write a program to calculate the scale factor for a given track and minimum radius so that the resulting track has the same length as the one of his original plan.
Bob made some drawings of the first test case:
|
|
|
Input Specification
The input starts with the number of test cases t (0 < t ≤ 100). Each test case starts with a line consisting of two integers: the minimal required radius r and the number of vertices n of the original track polygon (0 ≤ r ≤ 1 000; 3 ≤ n ≤ 10 000). Then, n lines follow, where each line specifies 2D-coordinates as two integers xi and yi (–10 000 ≤ xi, yi ≤ 10 000). (0,0) is the lower left corner. These are the coordinates of the original track's vertices in counterclockwise direction. You may safely assume that the area of the given polygon is not zero.
Output Specification
For each test case, print one line. If it is possible to construct a course according to the above description, output the scaling factor, otherwise output “Not possible”. The factor must have an absolute error smaller than 10–5.
Sample Input
220 510 0110 0130 200 1500 101 50 01 02 02 10 1
Output for Sample Input
0.730494Not possible