Kíváncsi bolhák

A legértékesebb tulajdonod egy bolhacirkusz, amelynek a fő attrakcióját hat akrobata bolha előadása jelenti. Egy nap véletlenül feldöntöd a bolhákat tároló dobozt, amelyek így mind leesnek a konyhád padlóját alkotó négyzet alakú csempék 4×4-es hálójára. Meglepő módon mindegyik bolha más-más csempén landol.

Andy fiadnak van egy (hagyományos, hatoldalú) kockája, amely pontosan akkora, mint egy csempe. Elhatározod, hogy játszol egy játékot. Először is lerakod a kockát pontosan egy olyan csempére, amelyen nincs bolha, majd elkezded forgatni a kockát az élein keresztül valamelyik szomszédos csempére. A bolhák nagyon kíváncsiak; szeretnek felfedezni. Ha olyan csempére forgatod a kockát, amelyen van egy bolha, akkor az felugrik a kocka aljára. A bolhák elég kicsik ahhoz, hogy elférjenek a kocka pöttyeinek vájataiban, tehát nem halnak meg a folyamat során. Hasonlóan, ha egy bolha van a kocka azon oldalán, amelyet a padlóra forgatunk, akkor az leugrik a kockáról a csempére.

A játék célja, hogy úgy forgassuk a kockát, hogy végül minden bolha a kockán legyen. A kocka nem hagyhatja el a konyhád 4×4-es csempehálóját. Az első példa bemenet egy lehetséges megoldását szemlélteti az alábbi ábra:

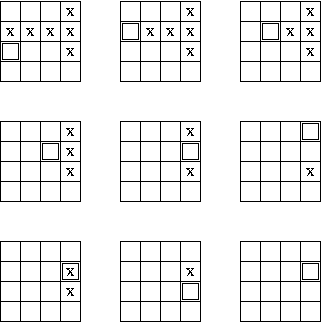
A bemenet specifikációja

A bemenet első sora a tesztesetek számát tartalmazza. Minden teszteset egy üres sorral kezdődik, amelyet 4 sor követ, mindegyikben 4 karakterrel. Ez a 4 sor a csempék kezdeti konfigurációját írja le. A „.” egy üres csempét, az „X” egy bolhát tartalmazó csempét jelöl, a „D” pedig a kockát tartalmazó csempét adja meg. Minden tesztesetben pontosan egy „D” és pontosan hat „X” karakter fog szerepelni.

A kimenet specifikációja

Minden tesztesetre egyetlen sort kell a kimenetre írni egy olyan számmal, amely megadja, hogy minimálisan hány forgatás szükséges ahhoz, hogy a kocka minden oldalán legyen egy bolha. Ha egy esetnek nincs megoldása, akkor az „impossible” szót kell kiírni.

Példa bemenet

1. 2
3. ...X
4. XXXX
5. D..X
6. ....
8. DX.X
9. .X..
10. ..X.
11. X..X

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. 8
2. 14

letöltés szöveges állományként