Pályasimítás

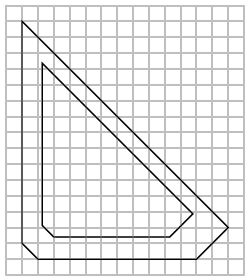
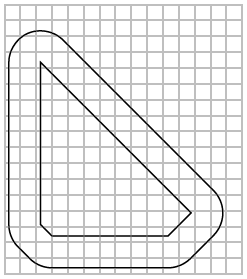
Bobnak azt a feladatot adták, hogy tervezzen egy adott hosszúságú versenypályát. Úgy gondolta, jó ötlet, ha egyszerűen létrehoz egy konvex sokszöget a megadott kerülettel. Azonban felvilágosították, hogy a versenyautók nem tudnak bevenni olyan éles kanyarokat, mint amilyenek a tervében szerepelnek.

Biztosítania kell tehát, hogy a pályája minden kanyarjának a sugara legalább egy megadott minimális sugár legyen. Bob szereti a pályája alakját, ezért nem akarja azt nagyon megváltoztatni. Az a terve, hogy lekicsinyíti a pályát középpontosan a sokszög súlypontja körül, majd az új pályát egy olyan vonallal rajzolja meg, amely konstans távolságra van a kicsinyített pályától. A választott távolságnak a legkisebb olyan távolságnak kell lennie, amely még megfelel az adott minimális sugárra vonatkozó követelménynek. Arra kér, hogy írj egy programot, amely adott pálya és minimális sugár esetén kiszámítja azt a kicsinyítési arányt, amellyel az eredményül kapott pálya hossza megegyezik az eredeti tervében szereplő pálya hosszával.

Bob készített pár rajzot az első tesztesetről:

1. ábra: Az eredeti és a lekicsinyített pálya.

2. ábra: A lekicsinyített és az eredményül kapott pálya.

A bemenet specifikációja

A bemenet t-vel, a tesztesetek számával kezdődik (0 < t ≤ 100). Minden teszteset első sorában két egész szám szerepel: r, az elvárt minimális sugár, és n, az eredeti pályához tartozó sokszög csúcsainak a száma (0 ≤ r ≤ 1 000; 3 ≤ n ≤ 10 000). Ezt n sor követi, amelyek mindegyike egy-egy 2D koordinátapárt (x_i és y_i) tartalmaz két egész számként (–10 000 ≤ x_i, y_i ≤ 10 000). A (0,0) a bal alsó sarok. Ezek az eredeti pálya csúcsainak a koordinátái az óramutató járásával ellentétes irányban felsorolva. Feltételezheted, hogy a megadott sokszög területe nem nulla.

A kimenet specifikációja

Minden tesztesetre egyetlen sort kell a kimenetre írni. Ha lehetséges a fenti leírásnak megfelelő pályát létrehozni, akkor a kicsinyítés arányát, ha nem, akkor a „Not possible” szöveget kell kiírni. A kicsinyítési arány abszolút hibájának kisebbnek kell lennie, mint 10^–5.

Példa bemenet

1. 2
2. 20 5
3. 10 0
4. 110 0
5. 130 20
6. 0 150
7. 0 10
8. 1 5
9. 0 0
10. 1 0
11. 2 0
12. 2 1
13. 0 1

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. 0.730494
2. Not possible

letöltés szöveges állományként