A Rational Sequence

A sequence of positive rational numbers is defined as follows:

An infinite full binary tree labeled by positive rational numbers is defined by:

• The label of the root is 1/1.
• The left child of label p/q is p/(p + q).
• The right child of label p/q is (p + q)/q.

The top of the tree is shown in the following figure:

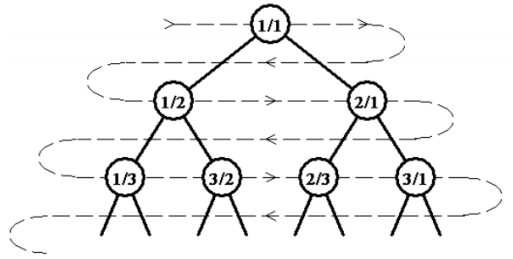
The sequence is defined by doing a level-order (breadth-first) traversal of the tree (indicated by the light dashed line). So that:

F(1) = 1/1, F(2) = 1/2, F(3) = 2/1, F(4) = 1/3, F(5) = 3/2, F(6) = 2/3, …

Write a program which finds the value of n for which F(n) is p/q for inputs p and q.

Input Specification

The first line of the input contains a single integer P (1 ≤ P ≤ 1000), which is the number of data sets that follow. Each data set should be processed identically and independently.

Each data set consists of a single line of input. It contains the data set number K, a single space, the numerator p, a forward slash (/), and the denominator q of the desired fraction.

Output Specification

For each data set, there is a single line of output. It contains the data set number K, followed by a single space, which is then followed by the value of n for which F(n) is p/q. Inputs will be chosen so that n will fit in a 32-bit integer.

Sample Input

1. 4
2. 1 1/1
3. 2 1/3
4. 3 5/2
5. 4 2178309/1346269

download as text file

Output for Sample Input

1. 1 1
2. 2 4
3. 3 11
4. 4 1431655765

download as text file