Programming contestsDEIK Regionális Programozó Csapatverseny, egyetemi/főiskolai kategória, 2016. december 4.
December 4, 2016, 10:10 AM –
December 4, 2016, 3:10 PM
|
Doors
Alex is a circle of radius R. Well, life as a circle is not easy. If he were a point, moving around and passing through doors would be effortless. But now he has to carefully inspect the surroundings before making every move.
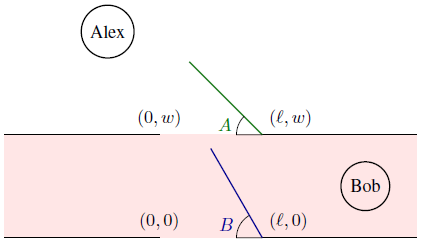
Alex is initially at position (0, y∞), where y∞ is much bigger than the width of the corridor w. Alex wants to meet Bob, who happens to be living to the far right of the corridor (may as well be somewhere at (x∞, w/2), where x∞ is much bigger than ℓ). The lengths of the two doors are ℓ. It is guaranteed that ℓ ≤ w, so that door B will never hit the opposite side of the wall.
You are given T scenarios. In each scenario, the angles A and B are given (both are radians in the range [0, π]). Find the largest r ≤ R such that when Alex's radius is shrunk to r, he can reach Bob while avoiding the obstacles (walls and doors).
Formally, Alex when shrunk to radius r can reach Bob if and only if there exists a (continuous) curve from (0, y∞) to (x∞, w/2) such that the minimal distance between a point on the curve and a point on an obstacle (a wall or a door) is at least r. In particular, if r = 0, then Alex will be able to reach Bob.
Input Specification
The first line of the input consists of three integers, R, ℓ, and w (1 ≤ ℓ, w, R ≤ 100 and ℓ ≤ w). The second line of the input consists of an integer T (1 ≤ T ≤ 10 000), the number of scenarios to follow. Each of the next T lines consists of a pair of real numbers, representing angles A and B (in radians). The numbers are given with exactly 4 decimal places.
Output Specification
For each scenario, output the required answer on a separate line. Your answer will be accepted if its absolute or relative error (compared to the judge's answer) is at most 10–5.
Sample Input
10 6 840.0000 0.00003.1415 0.00001.0472 0.00001.0472 1.5708
Output for Sample Input
0.0000000003.0000000002.5980798851.000000000