Ajtók

Alex egy R sugarú kör. Azonban körként az élet nem egyszerű. Ha pont lenne, a mozgás és az ajtókon való átjutás gond nélkül menne. Most viszont gondosan meg kell vizsgálnia a környezetét, mielőtt bármiféle mozgást végezne.

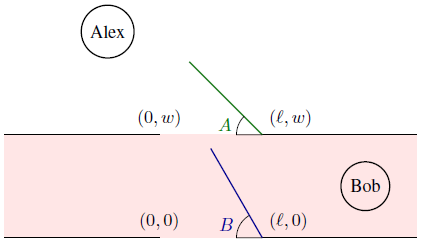
Alex kezdetben a (0, y_∞) pozícióban van, ahol y_∞ sokkal nagyobb, mint a folyosó szélessége (w). Alex szeretne találkozni Bobbal, aki történetesen messze a folyosó jobb oldalán lakik (lehet például az (x_∞, w/2) pozícióban, ahol x_∞ sokkal nagyobb, mint ℓ). A két ajtó hossza ℓ. Az garantált, hogy ℓ ≤ w, így a B ajtó sosem ütközik bele a szemközti falba.

Adott lesz T teszteset. Minden tesztesetben ismertek lesznek az A és B szögek (mindkettő radiánban a [0, π] tartományban). A feladatod, hogy meghatározd azt a legnagyobb r-et (r ≤ R), amelyre teljesül, hogy ha Alex sugarát r-re csökkentjük, akkor el tud jutni Bobhoz az akadályok (falak és ajtók) elkerülésével.

Formálisan: az r-re csökkentett sugarú Alex akkor és csak akkor tud eljutni Bobhoz, ha létezik egy (folytonos) görbe a (0, y_∞) és az (x_∞, w/2) pozíciók között úgy, hogy a görbe egy pontja és valamely akadály (fal vagy ajtó) egy pontja közötti minimális távolság legalább r. Ha r = 0, akkor Alex biztosan el tud jutni Bobhoz.

A bemenet specifikációja

A bemenet első sora három egész számot tartalmaz: R-et, ℓ-et és w-t (1 ≤ ℓ, w, R ≤ 100 és ℓ ≤ w). A bemenet második sorában egy T egész szám, a tesztesetek száma szerepel (1 ≤ T ≤ 10 000). A következő T sor mindegyike két valós számot tartalmaz, amelyek az A és B szögeket adják meg (radiánban). Ezek az értékek pontosan 4 tizedesjeggyel lesznek megadva.

A kimenet specifikációja

Minden tesztesetre a fent leírt választ kell a kimenetre írni külön sorban. A válaszod akkor lesz elfogadva, ha az abszolút vagy (a zsűri válaszához viszonyított) relatív hibája legfeljebb 10^–5.

Példa bemenet

1. 10 6 8
2. 4
3. 0.0000 0.0000
4. 3.1415 0.0000
5. 1.0472 0.0000
6. 1.0472 1.5708

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. 0.000000000
2. 3.000000000
3. 2.598079885
4. 1.000000000

letöltés szöveges állományként