Programozó versenyekDEIK Regionális Programozó Csapatverseny, középiskolai kategória, 2016. december 4.
2016. december 4. 10:10 –
2016. december 4. 15:10
|
Kém a metróban
Mariát, a titkosügynököt, Algorithms Citybe küldték, hogy teljesítsen egy különösen veszélyes küldetést. Számos izgalmas esemény után az Algorithms City Metro első állomásán találjuk őt, amint épp a menetrendet böngészi. Az Algorithms City Metro egyetlen vonalból áll, amelyen a vonatok mindkét irányban közlekednek, a menetrendje tehát nem túl komplikált.
Mariának egy helyi kémmel van találkája az Algorithms City Metro utolsó állomásán. Maria tudja, hogy egy nagy hatalmú szervezet van a nyomában. Azt is tudja, hogy egy állomáson várakozva nagy eséllyel elkaphatják. Sokkal biztonságosabb egy mozgó vonaton elrejtőzni, ezért elhatározza, hogy a lehető legtöbbet fog a vonatokon tartózkodni, még ha ez azzal is jár, hogy oda-vissza kell utazgatnia. Mariának tehát szüksége lenne egy olyan „útitervre”, amely eljuttatja őt az utolsó állomásra úgy, hogy időben odaérjen a találkájára, és közben a lehető legkevesebb várakozási időt töltsön az állomásokon. Írj egy programot, amely meghatározza a várakozások összidejét a legjobb útitervben!
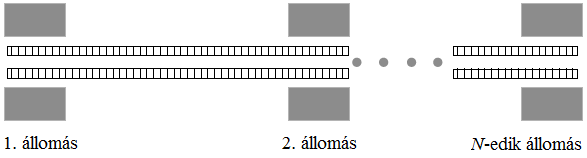
Az Algorithms City Metro rendszerében N állomás van, amelyek sorrendben 1-től N-ig vannak megszámozva. A vonatok mindkét irányban haladnak: az első állomástól az utolsó állomás felé, illetve az utolsó állomástól vissza az első felé. Adott két szomszédos állomás között a vonatok mindig ugyanannyi idő alatt közlekednek, mert minden vonat azonos sebességgel halad. A vonatok nagyon rövid ideig állnak az egyes állomásokon, ezt az időt az egyszerűség kedvéért figyelmen kívül hagyhatjuk. Mivel Maria nagyon gyors ügynök, mindig át tud szállni a másik vonatra egy állomáson, még akkor is, ha a két vonat az adott állomáson azonos időpontban áll meg.
A bemenet specifikációja
A bemenet számos tesztesetet tartalmaz. Minden teszteset hét sorból áll az alábbi információkkal:
1. sor: Egy N egész szám (2 ≤ N ≤ 50), az állomások száma.
2. sor: Egy T egész szám (0 ≤ T ≤ 200), a találka időpontja.
3. sor: N – 1 egész szám: t1, t2, …, tN – 1 (1 ≤ ti ≤ 20), amelyek a vonatok utazási idejeit adják meg két-két szomszédos állomás között; t1 az első két állomás közötti utazási idő, t2 a második és harmadik állomás közötti utazási idő, stb.
4. sor: Egy M1 egész szám (1 ≤ M1 ≤ 50), az első állomásról induló vonatok száma.
5. sor: M1 egész szám: d1, d2, …, dM1 (0 ≤ di ≤ 250 és di < di + 1), amelyek az első állomásról induló vonatok indulási idejeit adják meg.
6. sor: Egy M2 egész szám (1 ≤ M2 ≤ 50), az N-edik állomásról induló vonatok száma.
7. sor: M2 egész szám: e1, e2, …, eM2 (0 ≤ ei ≤ 250 és ei < ei + 1), amelyek az N-edik állomásról induló vonatok indulási idejeit adják meg.
Az utolsó tesztesetet egy olyan sor követi, amely egyetlen nullát tartalmaz.
A kimenet specifikációja
Minden tesztesetre egyetlen sort kell a kimenetre írni, amely a teszteset (1-ről induló)
sorszámát tartalmazza, majd a várakozások összidejét a legjobb útitervben, vagy pedig az
„impossible” szót, ha Maria nem érhet oda a találkára. Kövesd
pontosan a példa kimenetben látható formátumot!
Példa bemenet
4555 10 1540 5 10 2040 5 10 154181 2 350 3 6 10 1260 3 5 7 12 152302012071 3 5 7 11 13 170
A példa bemenethez tartozó kimenet
Case Number 1: 5Case Number 2: 0Case Number 3: impossible