Programozó versenyekDEIK Regionális Programozó Csapatverseny, középiskolai kategória, 2017. december 3.
2017. december 3. 10:10 –
2017. december 3. 15:10
|
A — Az okos nyíl
Egy darts játékban a játék megkezdése előtt a játékosok véletlenszerűen dobálnak nyilakat egy darts táblára. Minden nyíl más-más pozícióba kerül. Amikor elkezdődik a játék, a szabályok szerint minden körben egy játékos egy új nyilat dob, mondjuk az (x,y) pozícióba. A kör pontszámának meghatározásához az új nyíl (x,y) pozíciójához legközelebb eső két régi nyilat kell felhasználni. Legyen az új nyílhoz legközelebbi két régi nyíl pozíciója (x1,y1) és (x2,y2)! A pontszám ekkor a következő képlettel számítható ki:
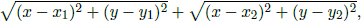
azaz a pontszám az (x,y) pozíció és a két legközelebbi régi nyíl euklideszi távolságának az összege. A játék megnyeréséhez minden körben minimalizálni kell a pontszámot.
A játék előtti régi nyilak pozícióinak az ismeretében határozd meg, hogy mekkora a legkisebb elérhető pontszám az első körben!
A bemenet specifikációja
A bemenet első sora egy N egész számot tartalmaz, amely a tesztesetek számát adja meg. Minden teszteset első sorában egy D egész szám, a darts táblán lévő régi nyilak száma szerepel (2 ≤ D ≤ 5000). A következő D sor mindegyike egy-egy régi nyíl (x,y) pozícióját tartalmazza, ahol x és y fehér karakterekkel elválasztott egész számok, melyekre 0 ≤ x, y ≤ 224. A darts táblán minden nyíl más-más pozícióban van.
A kimenet specifikációja
Minden tesztesetre a minimális pontszámot kell a kimenetre írni külön sorban, két tizedesjeggyel, a második tizedesjegyre csonkítva. Például mind a 3.412, mind a 3.419 értékű pontszám 3.41 formában jelenjen meg a kimeneten!
Példa bemenet
251 02 04 01 23 251 14 12 35 23 6
A példa bemenethez tartozó kimenet
1.001.41