Programming contestsDEIK Regionális Programozó Csapatverseny, középiskolai kategória, 2017. december 3.
December 3, 2017, 10:10 AM –
December 3, 2017, 3:10 PM
|
A — Shooting a Smart Dart
In a dart game, before a game begins, players randomly shoot many darts onto the dartboard. No two darts share the same position. When the game begins, the game rule is that in each round, a player shoots a new dart, say onto position (x,y). The two old darts (being already on the dartboard) closest to the new dart at (x,y) are used to help determine the score of the round. Let the positions of the two closest old darts be (x1,y1) and (x2,y2). The score is
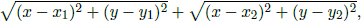
that is, the sum of the Euclidean distances between (x,y) and the two closest old darts. To win the game, you need to minimize the score in each round.
Given the positions of the old darts before the game, compute the minimum score a player can get in the first round.
Input Specification
The first line of the input contains an integer N, which is the number of test cases. The first line of each test case contains an integer D (2 ≤ D ≤ 5000), which is the number of old darts on a dartboard. Each of the next D lines gives the position (x,y) of an old dart on the dartboard, where x and y are integers separated by a whitespace, 0 ≤ x, y ≤ 224. No two darts have the same position on the dartboard.
Output Specification
For each test case, output on a single line the minimum score, truncated to the second decimal place. For example, 3.412 and 3.419 would both truncate to 3.41.
Sample Input
251 02 04 01 23 251 14 12 35 23 6
Output for Sample Input
1.001.41