Programming contestsECN programozó csapatverseny, 2018. május 12.
May 12, 2018, 10:15 AM –
May 12, 2018, 3:15 PM
|
Circular Matrix Matching
A p × r matrix B = (Bij)0 ≤ i < p, 0 ≤ j < r occurs in m × n matrix A = (Aij)0 ≤ i < m, 0 ≤ j < n starting at position (k, l) if Bij = Ak + i, l + j for 0 ≤ i < p, 0 ≤ j < r, and m, n, p, r > 0, where the indices are considered circularly. For example, let:
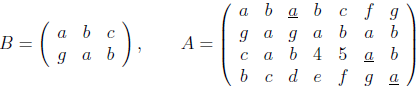
B occurs in A beginning at positions: (0, 2), (2, 5), and (3, 6) (positions of underlined elements in the matrix).
For given B and A, find all starting positions at which B occurs in A.
Input Specification
The first line of the input contains the number of test cases. For each test case, the first line contains the number of rows p and the number of columns r for matrix B, separated by a space. Each of the next p lines contains the elements of a row of matrix B, each element being a character, separated by a space. The next line contains the number of rows m and the number of columns n for matrix A, separated by a space. Each of the next n lines contains the elements of a row of matrix A, each element being a character, separated by a space.
Input Limits and Constraints
- 1 ≤ p ≤ 100, 1 ≤ r ≤ 100, 1 ≤ m ≤ 100, 1 ≤ n ≤ 100;
- each matrix element is a character.
Output Specification
For each test case, print in a line #i, where i is the number
of the test case, followed by a line containing the found positions in lexicographic order in
the form (k,l), separated by a space. If there is no solution, leave a
blank line.
Sample Input
22 3a b cg a b4 7a b a b c f gg a g a b a bc a b 4 5 a bb c d e f g a2 2a aa a5 5a a a a aa a a a aa a a a aa a a a aa a a a b
Output for Sample Input
#1(0,2) (2,5) (3,6)#2(0,0) (0,1) (0,2) (0,3) (0,4) (1,0) (1,1) (1,2) (1,3) (1,4) (2,0) (2,1) (2,2) (2,3) (2,4) (3,0) (3,1) (3,2) (4,0) (4,1) (4,2)