Programming contestsAndy Poe's Faculty Seminar, June 7, 2018
June 7, 2018, 1:00 PM –
June 7, 2018, 5:00 PM
|
Beevaria
An eastern European country called Beevaria is setting up a new jail. It is an unusual jail in that all of the cells are made with walls that are clear and unbreakable. The government wants to cut costs and, as such, has selected an unusual jail cell arrangement: each cell is a hexagon. The government has contracted with a construction firm to make these jails in various parts of the country using standardized materials. All that the construction firm needs to know is the size of the building, which the government specifies using the number of cells across the top.
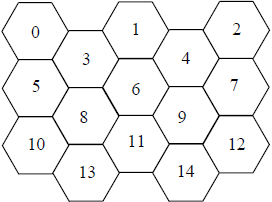
Consider the figure above. The size of this jail is S = 3, consisting of 3 alternating pairs of rows starting with 3 hexagons and then 2 hexagons each, i.e., 3, 2, 3, 2, 3, 2. If the construction crew builds a jail of size S = 2, the arrangement is 2, 1, 2, 1. For S = 4, it is 4, 3, 4, 3, 4, 3, 4, 3. Each cell also has a number, as shown in the diagram. The numbering scheme matches the value for S, of course, so that for S = 5, the first row contains 0..4, the second contains 5..8, etc.
Beevaria never has many criminals; jails are rarely full. In fact, a prison is never so full that the number of prisoners plus guards exceeds the number of cells. In the interests of saving money, the Beevaria government has opted to only supply a sufficient number of guards as needed to watch all of the prisoners. Since the walls are clear, this makes sense; if there is a prisoner in cell 13 and another in cell 14, only one guard is needed as long as the guard sits in cell 11. That guard can see both prisoners at the same time. Guards can only see into cells that are along a line of sight perpendicular to any of the six glass walls of the cell where they are located. For instance, the guard in cell 11 can watch 1, 5, 6, 7, 8, 9, 13, and 14 but cannot watch 0, 2, 3, or 4, for instance.
Both a guard and a prisoner cannot occupy a cell: these prisoners may be dangerous criminals!
Examples
Here are some combinations to think about, using the S = 3 diagram from above:
| Prisoners: |
0, 1, 2 1, 4, 5 9, 11, 13 5, 6, 12, 13 0, 5, 9, 10, 12 2, 4, 6, 8, 10 |
Guard position(s): |
6 6, 11 7 3 3, 8 1, 5, 7 |
(for example, also others) (note that the guard can see all three) (for example, also 3, 4, and others) (for example) |
The problem
When presented with a value for prison size S and a set of cell numbers for prisoners, determine the minimum number of guards that are needed to keep watch over all of the prisoners.
Input Specification
There will be multiple prison descriptions in the input. Each description gives the prison size S and the numbers of the cells housing prisoners. The input is a sequence of integers, one per line. The integer on the first line of a description specifies the size S of a prison, which is never larger than 25. This is followed by one line for each prisoner in the prison giving the prisoner’s cell number. A –1 (on a line by itself) follows the cell number for the last prisoner, and a –1 (on a line by itself) follows the last prison description in the input.
Output Specification
For each input prison description, print the prison number (1, 2, …) and the number of guards needed to watch the prisoners in the format shown below. Display a blank line after the output for each prison.
Sample Input
30591012-13246810-1-1
Output for Sample Input
Prison 1, Guards needed: 2Prison 2, Guards needed: 3