Aranymetszés

Az aranymetszés vagy aranyarány egy olyan arányosság, ami a természetben és művészetben is gyakran megjelenik, természetes egyensúlyt teremtve a szimmetria és az aszimmetria között.

Aranymetszési arányok találhatók számos ókori épületen, középkori és reneszánsz képzőművészeti alkotásokon. Az ókori püthagoreusok (Püthagorasz és követői), akik szerint a valóság matematikai alapokon nyugszik, az aranymetszésben a létezés egyik alaptörvényét vélték felfedezni, ugyanis ez az arány felismerhető a természetben is (például az emberi testen vagy csigák mészvázán).

Az aranymetszés arányait tartalmazó formák máig nagy esztétikai értékkel bírnak, számos területen (például a tipográfiában vagy a fényképészetben) alkalmazzák őket.

Két rész (a és b, a > b) az aranymetszés szerint aránylik egymáshoz, ha az egész (a + b) úgy aránylik a nagyobbik részhez (a-hoz), ahogy a nagyobbik rész (a) a kisebbik részhez (b-hez):

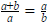
Vagyis a nagyobbik rész egyenlő az összeg és a kisebbik rész mértani közepével:

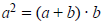
A definícióból kiszámolható, hogy a nagyobb rész (a) hányszorosa a kisebb résznek (b-nek), tehát megkapható az a Φ szám, amelyre 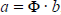, másképpen 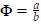teljesül.

A definíció szerint

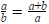
A jobb oldali tört számlálóját és nevezőjét is b-vel elosztva:

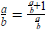
Ebbe 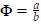-t behelyettesítve kapjuk, hogy

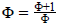
Φ-vel szorozva, majd 0-ra rendezve:

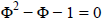
Ezt a másodfokú egyenletet megoldhatjuk a megoldóképlettel:

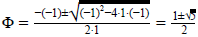
Az egyenlet negatív gyöke (≈ –0,618) a feladat jellege miatt nem megoldása a problémának, így:

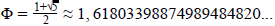
Az aranyarányt numerikusan kifejező irracionális Φ számnak (görög nagy fí) számos érdekes matematikai tulajdonsága van, ezeket már nem fejtjük ki bővebben, viszont felhívjuk a figyelmét a Wikipédia Aranymetszés szócikkére, ahonnan a feladat alapötletét adó szöveg is származik.

Mivel Φ irracionális, ezért senki nem tud két olyan pozitív egész számot mondani, amelyeknek a hányadosa megegyezne Φ-vel, de arra van esély, hogy tetszőlegesen kicsiny legyen e hányados és Φ értéke között a távolság.

Az ön feladata, hogy írjon egy programot, amely a standard bemenet első sorából beolvas egy egész számot (N-et), ez a Φ értékét megtippelő iskolások száma! A bemenet következő N sorában iskolások adatai szerepelnek, soronként egy-egy, a következő formában:

név:nagyobb_szám:kisebb_szám

A név egy sztring, a nagyobb_szám és a kisebb_szám két pozitív egész érték, amelyekre teljesül a nagyobb_szám > kisebb_szám egyenlőtlenség. A programja rendezze az iskolások adatait tippjeiknek a Φ értékétől való távolságának nagysága szerint növekvő sorrendbe, azaz a felsorolásban legelöl szerepeljenek azoknak az iskolásoknak az adatai, akik a legjobban tudták megtippelni Φ értékét! Ha több iskolás esetében is azonos lenne ez a távolság, akkor az ő adataikat neveik lexikografikusan növekvő sorrendjében írja a standard kimenetre, soronként egyet-egyet, a példa kimenetben látható formában!

Példa bemenet

1. 8
2. Anna:4:2
3. Botond:2:1
4. Cecilia:5:3
5. Dominik:9:5
6. Elek:13:8
7. Ferenc:22:13
8. Gergely:33:21
9. Hedvig:54:34

letöltés szöveges állományként

A példa bemenethez tartozó kimenet

1. Elek: 13/8
2. Hedvig: 54/34
3. Gergely: 33/21
4. Cecilia: 5/3
5. Ferenc: 22/13
6. Dominik: 9/5
7. Anna: 4/2
8. Botond: 2/1

letöltés szöveges állományként