Champagne Pyramid

After the successful preparation of the ECN contest, the organizers decided to open a bottle of champagne. One of the organizers came up with the idea to build a three-dimensional pyramid from the drinking glasses (see the figure above) and fill the glass on the top of the pyramid until every glass is full of champagne. Interestingly, all the glasses look the same, but they have different volumes. Constructing the pyramid, there are the following rules:

The levels of the pyramid are numbered from 1 (on the top) to n (on the bottom).
Except for the lowest (nth) level, every glass is placed on exactly 4 glasses below it.
On the ith level, there are i × i glasses.
The glasses are numbered following the rule on the following figure:

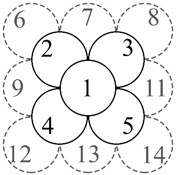
Once the gigantic pyramid is built, the organizers quickly open the bottle and start filling the top glass. The filling speed is exactly 1 drop per second. As a glass is filled, something funny happens. The first drop that hits the filled glass goes on to the lower level into the glass to the northwest (NW), the second drop to the northeast (NE), the third to the southeast (SE), and the fourth to the southwest (SW). The rule applies further on: the fifth drop goes on to the NW, the sixth to NE, the seventh to SE, the eighth to SW, etc. For example, in the figure above, when the 1st glass becomes full, the drops will go on into the 2nd, 3rd, 5th, and 4th glass in this order, concentrically. Another example, when the 4th glass becomes full, the drops go on concentrically to the 9th, 10th, 13th, and 12th glass.

It has also been observed by the organizers that some of the glasses at the lowest level are filled in some cases sooner than the others, and some drops of champagne spill on the table.

Knowing that the organizers don't want to waste the champagne on the table, they thought they would first calculate the number of wasted drops of champagne, and only then decide whether to make this spectacular pyramid or not. The organizers are tired, and they ask you to write a program for them that, knowing the number of levels n and the volume of each glass V_i, calculates the minimum number of seconds needed for all the glasses to become full and the number of wasted drops at that moment.

Input Specification

The first line of the input contains one integer n, which is the number of levels of the pyramid (1 ≤ n ≤ 25).

The next line contains m = n(n + 1)(2n + 1) / 6 numbers: V₁, V₂, …, V_m, the volumes of each glass, measured in drops (1 ≤ V_i ≤ 25, i = 1, …, m). The numbering of the glasses follows the rule mentioned above.

Output Specification

Output two numbers in a single line separated by a space. The first number is the minimum time in seconds needed for all the glasses to become full, and the second number is the number of champagne drops that spill on the table.