Plenty of Fish

The nature reserve of Lake Tisza is the home of K species of fish. There are N prominent habitats at different spots over the lake, where fishes can be found in great abundance — for simplicity, let us assume that each habitat houses a single species of fish.

The lake is also a favourite place of fishermen. To preserve the richness of nature, fishing in the lake is regulated: fishing is allowed only near the southern shore, inside a rectangular area specified by the Fishing Association. For this problem, let the x-axis of the Cartesian plane represent the shore of the lake, and the points above it represent the lake itself. Suppose that the fishing area is an axis-aligned rectangle and its bottom side rests on the x-axis.

Recently, there is a gossip that the Office for Environmental Protection wants to ban the fishing of one of the species — but no one knows which one yet! If this happens, the Association must be ready to select a new fishing area: one that has no habitats of the banned species at all. On the other hand, they want to choose an area containing as many habitats of any other (non-banned) species as possible.

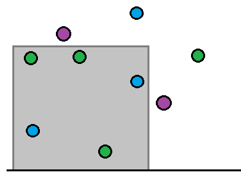
An optimal fishing area (containing 5 habitats) when the species denoted by purple is banned.

The association wants you to help them prepare for each possible scenario. Your task is to determine for each species of fish that, if it was banned, then what is the maximal number of habitats an optimally selected fishing area could contain.

Input Specification

The first line of the input contains the number of test cases T.

Each test case starts with a line containing the number of habitats N (2 ≤ N ≤ 200 000) and the number of species K (2 ≤ K ≤ N). The next N lines denote the positions of habitats (x_i, y_i) and the species s_i dwelling in the habitat (1 ≤ x_i, y_i ≤ 10⁹, 1 ≤ s_i ≤ K).

It is guaranteed that for each species, there is at least one habitat housing it, and that the total number of habitats over the T testcases does not exceed 10⁶.

Output Specification

For each test case, print a single line containing K integers: the i-th being the maximal number of habitats an optimally chosen fishing area can contain in the case when fishing the i-th species is banned.

Sample Input

1. 1
2. 9 3
3. 1 2 1
4. 1 5 2
5. 3 6 3
6. 4 5 2
7. 5 1 2
8. 6 4 1
9. 6 7 1
10. 7 3 3
11. 9 5 2

download as text file

Output for Sample Input

1. 3 3 5

download as text file

The example corresponds to the figure in the task statement.