Graphs With a Special Labeling Property

In many distinct areas of mathematics, as a result of deep characterization theorems, surprisingly arrive — nobody knows exactly why — the same special graphs. A very simple instance in which these graphs also appear, is the next one.

Take a simple connected graph and label its vertices with positive integers in such a way that the double of each number minus 2 is equal to the sum of the neighbouring numbers. It turns out that such a labeling is never possible, except for a few very special graphs. These graphs are the members of two infinite family, having n vertices, named A_n (n ≥ 2) and D_n (n ≥ 4), shown below with the proper labeling, and surprisingly enough, three more singular graphs, having 6, 7, and 8 vertices respectively, named E₆, E₇, and E₈, shown below without their labeling.

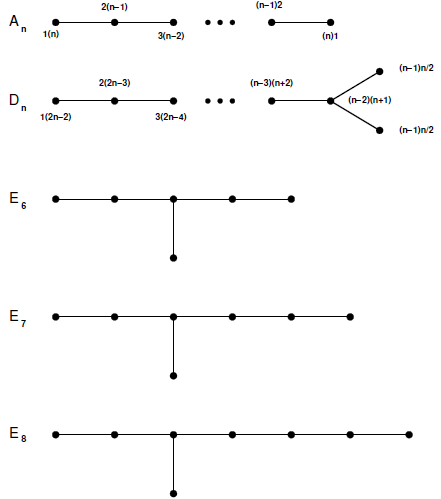
Your task is to compute the proper labeling of these last three graphs.

Input Specification

There is no input for this problem.

Output Specification

Output three lines, each containing an integer, the sum of the labels of E₆, E₇, and E₈, respectively.