Mr. G and Mr. D

Mr. G and Mr. D want to traverse a square matrix of size n × n in horizontal (left to right or vice versa) or vertical (top to bottom or vice versa) directions. The cost of a crossing is equal to the sum of the numbers on the chosen route. The horizontal crossing is made through the area indicated in figure A, and the vertical one according to figure B. The crossing rules are as follows: (i) the route starts at the border of the matrix (first/last row or first/last column), (ii) at each step, it forwards a row or a column, (iii) the consecutive cells on the route must be adjacent (they have a common side or corner). Mr. D is able to find the optimal path in the chosen direction (the sum of the numbers in the crossed cells is minimal). On the other hand, Mr. G follows a simplistic method: (i) he chooses the cell with the minimum value on the starting row / column, (ii) at each step, he chooses the neighboring cell with the minimum value. The advantage of Mr. G is that being faster he chooses the crossing direction firstly. For example, if Mr. G chooses horizontal crossing (from left to right or vice versa), then Mr. D must cross the matrix in the vertical direction (from top to bottom or vice versa).

Is there a guarantee that Mr. D can cross the matrix at a lower cost than Mr. G?

Input Specification

The first line of the input contains n, the size of the square matrix (1 < n < 100, n is odd). Each of the next n lines contains n positive integers (≤ 100), separated by one or more spaces, giving the elements of the matrix.

Output Specification

Print one line to the standard output, containing “YES” if Mr. D can cross the matrix at a lower cost than Mr. G, otherwise “NO”.

Sample Input

1. 5
2. 1 2 4 5 6
3. 8 9 3 5 6
4. 2 8 6 6 3
5. 7 3 5 9 2
6. 9 4 6 3 1

download as text file

Output for Sample Input

1. YES

download as text file

Explanation

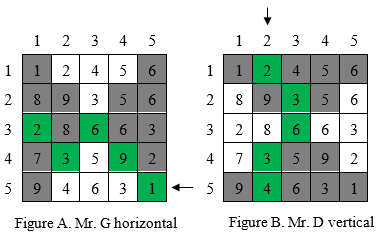
One example for the cost of crossing the matrix horizontally (from right to left) for Mr. G is 21 (Figure A. Mr. G horizontal), while for Mr. D, the cost of crossing the matrix vertically from bottom to top can be 18 (Figure B. Mr. D vertical).

Vice versa, if Mr. G crosses the matrix vertically from bottom to top, the cost is 21 (Figure B. Mr. G vertical), while for Mr. D, crossing horizontally from left to right, the sum is 19 (Figure A. Mr. D horizontal).

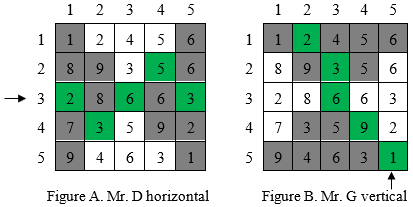
In both cases, Mr. D can cross the matrix at a lower cost than Mr. G, therefore the expected output is “YES”.