Programming contestsDEIK Regionális Programozó Csapatverseny, középiskolai kategória, 2022. december 4.
December 4, 2022, 10:00 AM –
December 4, 2022, 3:15 PM
|
ski
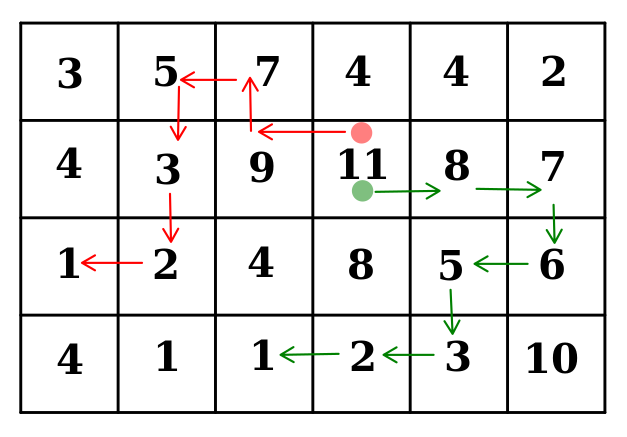
The figure above represents a simplified map of some highland in a form of a matrix.
The numbers show the altitudes of the locations. We like skiing and we are searching for
a good path. A path through the highland is called good if the subsequent locations are
horizontally or vertically (but not diagonally) adjacent and each of them has a
strictly lower altitude than the previous one.
In the figure the path that starts at 11 and follows the green arrows, is a sequence of the locations
(2,4),(2,5),(2,6),(3,6),(3,5),(4,5),(4,4),(4,3), where the first and second
number are the row and column index respectively.
Easy to verify that it is a good path, as well as the red one is. The length of
a path is the number of locations in it.
The green path is of length 8 and the red one is of length 7.
Your task is to compute the length of the longest good path for a given map.
Input Specification
R C
t11 ... t1C
t21 ... t2C
...
tR1 ... tRC
The comma separated numbers 1 ≤ R,C ≤ 100 in the first row are the number of rows and columns
of the map - respectively. In each of the subsequent R rows there are C
comma separated positive integers, not larger than 106 .
Output Specification
L
A single line with length L of the longest good path.
Sample Input 1
2 21 23 4
Sample Output 1
3
Sample Input 2
3 41 2 3 34 5 4 27 6 5 6
Sample Output 2
7
Sample Input 3
4 63 5 7 4 4 24 3 9 11 8 71 2 4 8 5 64 1 1 2 3 10
Sample Output 3
8