Egyptian Fractions

Mathematics is ancient. Very ancient. Imagine yourself more than 3500 years ago in ancient Egypt. An Egyptian fraction is a finite sum of distinct unit fractions, like this:

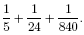
The sum of these fractions is ¹⁷⁄₇₀. It may not be immediately evident that every fraction can be represented as a sum of distinct unit fractions, making it, too, an Egyptian fraction. However, these decompositions are not necessarily unique. For instance,

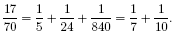
The practicality of Egyptian fractions becomes apparent when you imagine the scenario of paying ¹⁷⁄₇₀ of a quantity. Instead of repeating the fraction ¹⁄₇₀ 17 times, the Egyptians devised a more efficient approach. By preparing in advance some unit fractions, they could simply present two of them: ¹⁄₇ and ¹⁄₁₀. This demonstrates how the use of Egyptian fractions offered a more practical solution in such situations. While the use of Egyptian fractions proved practical in certain scenarios, a drawback arises from the challenge of decomposing a fraction into a sum of distinct unit fractions. Many related questions remain open today. For instance, there is a conjecture, not yet proven, suggesting that for every n ≥ 5, the fraction 4/n can be decomposed into a sum of not more than 3 unit fractions (Erdős–Straus conjecture, verified up to n < 10¹⁷).

A natural question arises: given a fraction, what is the minimum number of unit fractions in its Egyptian number representation? Currently, it remains unknown whether a polynomial time algorithm exists for this problem, and the computational complexity is also uncertain. While we can resort to a brute-force search for computation, it's an open challenge to devise a more efficient algorithm.

Your task now is to design an algorithm capable of computing the Egyptian fraction representation(s) of a given fraction with the fewest possible terms. Assume the fraction is composed of positive integers and has a value less than 1. Your goal is to compute all its expansions as a sum of unit fractions with the minimum number of terms.

Input Specification

The input contains several lines, each has a fraction written in the form a/b, where a and b are positive integers, 0 < a < b.

Output Specification

The output should have the same number of lines as the input. For each input line, print one line to the output, containing a number, the minimum number of unit fractions, followed by the space-delimited denominators of the minimum-length expansion enclosed in parentheses. If the expansion is not unique, additional denominators should be listed after a comma and a space. Ensure that the denominators and parentheses are ordered in increasing lexicographical order for each line.

Sample Input

1. 33/182
2. 223/12342
3. 511/1404

download as text file

Output for Sample Input

1. 2 (7 26)
2. 2 (102 121)
3. 3 (3 36 351), (4 9 351), (4 13 27)

download as text file