Carpathian Riders

Carpathian Riders is a famous motorcycle gang and competitive programming club. They decided to participate in the upcoming ECN Sapientia programming contest, travelling there on their bikes. To get to the contest venue, they must cross the Carpathian Mountains.

The Carpathians is a grid of R rows and C columns. Each cell has an elevation value between 0 and 1000, inclusive. Some cells are not passable on motorbikes – those cells are marked with the elevation value –1.

The gang can enter the Carpathians at any passable cell on the western edge of the grid and leave the mountains at some cell on the eastern edge. They travel from the west to the east in multiple steps. In each step, they can move to the cell either directly to the east, or diagonally to the northeast, or diagonally to the southeast. Each cell that they visit must be passable.

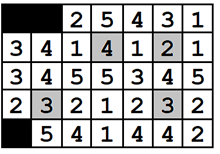
A sample grid representing the Carpathian Mountains.

The gang does not want to be late from the contest, so they try to avoid riding up to cells with high elevation: the sum of elevations during the trip must be minimized.

Sounds easy enough? Well, there's a catch. Since this is a motorcycle gang, they love visiting mountain passes. A mountain pass is a grid cell that has a strictly greater elevation value than the two cells to its east and west, but has a strictly lower elevation value than the two cells to its north and south. Cells on the edges of the grid cannot be mountain passes, similarly to cells adjacent to impassable cells. In the example above, all cells that are mountain passes are shaded in grey.

The bikers decided that they want to visit exactly P passes along the trip. Your task is to help them planning a trip from the west to the east which contains exactly P passes, avoids impassable cells and the sum of elevations is minimized.

Input Specification

The first line of the input contains the number of rows and columns R and C (3 ≤ R, C ≤ 500) and the exact number of passes to visit P (0 ≤ P ≤ 10).

Each of the next R lines contains C elevation values. Impassable locations are represented by –1, and all other elevations are between 0 and 1000, inclusive. There is at least one cell on the western and one cell on the eastern edge of the grid that are passable.

Output Specification

Print one line to the standard output, containing the sum of elevations along an optimal trip with exactly P passes. If no such trip exists, output the string “impossible”.